Reptation

Reptation is the snake-like thermal motion of very long linear, entangled macromolecules in polymer melts or concentrated polymer solutions.

Entanglement means the topological restriction of molecular motion by other chains.

The concept of reptation was introduced into polymer physics in 1971 by Pierre-Gilles de Gennes^[1] to explain the dependence of the mobility of a macromolecule on its length. It is used as a mechanism to explain the viscous flow in an amorphous polymer.

Mechanism

Entangled polymers are characterized with effective internal scale, commonly known as ‘the length of macromolecule between adjacent entanglements’ M_e.

Effective cross-links from entanglements with other polymer chains restrict polymer chain motion to a 'tube' within these restrictions. Since polymer chains would have to be broken to allow the restricted chain to pass through them, the mechanism for movement (flow) of this restricted chain is reptation. In the 'blob' model, the polymer chain is made up of $n$ Kuhn lengths of individual length $l$ . 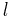The chain is assumed to form tangled 'blobs' between each effective cross-link, containing 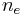$n_{e}$ Kuhn length segments in each. The mathematics of random walks can show that the average end-to-end length of a polymer chain, made up of 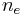$n_{e}$ Kuhn lengths is 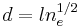$d=l n_{e}^{1/2}$ . Therefore if there are $n$ total Kuhn lengths, and $A$ blobs on a particular chain:
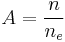
$A= \dfrac{n}{n_{e}}$
The total end-to-end length of the restricted chain $L$ is then:
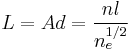
$L=Ad= \dfrac{nl}{n_{e}^{1/2}}$
This is the average length a polymer molecule must diffuse to escape from its particular `tube', and so the characteristic time for this to happen can be calculated using diffusive equations. A classical derivation gives the reptation time $t$ :
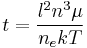
$t=\dfrac{l^2 n^3 \mu}{n_{e} k T}$
where $\mu$ is cofficient of friction on a particular polymer chain, $k$ is Boltzmann's constant, and $T$ is the absolute temperature.
The linear macromolecules reptate, if the length of macromolecule M is bigger than ten times ‘the length of macromolecule between adjacent entanglements’ M_e . There is no reptation motion for polymers with M<10 M_e, so that the point 10 M_e is a point of dynamic phase transition. Due to the reptation motion the coefficient of self-diffusion and conformational relaxation times of macromolecules depend on the length of macromolecule as M⁻² and M³, correspondingly.^[2]^[3] The conditions of existence of reptation in the thermal motion of macromolecules of complex architecture (macromolecules in the form of branch, star, comb and others) have not been established yet.

The dynamics of shorter chains or of long chains at short times is usually described by the Rouse model.

To be merged

Reptation theory describes the effect of polymer chain entanglements on the relationship between molecular mass and chain relaxation time (or similarly, the polymer’s zero-shear viscosity). The theory was originally developed in 1971 by Pierre-Gilles de Gennes, and has since been evolved by Sir Sam Edwards and Masao Doi. As the name suggests, the theory envisions the movement of entangled polymer chains as analogous to snakes slithering through one another. The theory predicts that, in entangled systems, the relaxation time τ is proportional to the cube of molecular mass. This is a reasonable approximation of the actual observed relationship, τ~(Molecular Mass)^3.4 .

The prediction of the theory is arrived at by a relatively simple argument. First, each polymer chain is envisioned as occupying a tube of length L, through which it may move with snake-like motion (creating new sections of tube as it moves). Furthermore, if we consider a time scale comparable to τ, we may focus on the overall, global motion of the chain. Thus, we define the tube mobility as μ_tube=v/f , where v is the velocity of the chain when it is pulled by a force f. Note also that μ_tube will be inversely proportional to the degree of polymerization (and thus also inversely proportional to chain weight).

The diffusivity of the chain through the tube may then be written as D_tube=k_BTμ_tube. By then recalling that in 1-dimension the mean square displacement due to Brownian motion is given by s(t)² = 2D_tubet, we obtain s(t)²=2k_BTμ_tubet. The time necessary for a polymer chain to displace the length of its original tube is then t=L²/(2k_BTμ_tube). By noting that this time is comparable to the relaxation time , we establish that τ~L²/μ_tube. Since the length of the tube is proportional to the degree of polymerization, and μ_tube is inversely proportional to the degree of polymerization, we observe that τ~(DP_n)³ (and so τ~(Molecular Mass)³).

From the preceding analysis, we see that molecular mass has a very strong effect on relaxation time in entangled polymer systems. Indeed, this is significantly different from the untangled case, where relaxation time is observed to be proportional to molecular mass. This strong effect can be understood by recognizing that, as chain length increases, the number of tangles present will dramatically increase. These tangles serve to reduce chain mobility. The corresponding increase in relaxation time can result in viscoelastic behavior, which is often observed in polymer melts.^[4]

References

^ De Gennes P.G. Reptation of a polymer chain in the presence of fixed obstacles. J. Chem. Phys. 55, 572 - 579 (1971).
^ Pokrovskii V.N. A justification of the reptation-tube dynamics of a linear macromolecule in the mesoscopic approach. Physica A 366, 88-106 (2006).
^ Pokrovskii V.N. The reptation and diffusive modes of motion of linear macromolecules. J. Exper. Theor. Phys. 106 (3), 604-607 (2008).
^ Pokrovskii V.N. The mesoscopic theory of polymer dynamics. The second ed., Springer, 2010.